问题 :所谓数学题型教学法,是否使学生变得机械化,从而不利思想开发呢?
回答:
 1、提取模块而非零碎知识点
1、提取模块而非零碎知识点 2、稳中求变
2、稳中求变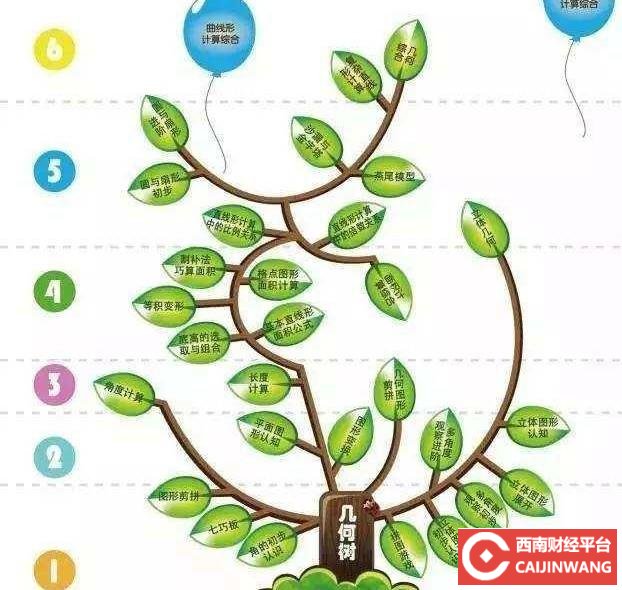 写在最后,是让学生记忆零散的知识点,再慢慢地形成自己知识体系。还是把知识点整体化放在习题中记忆,更有利于学生知识的提取呢?需要老师根据自己的教学风格调节二者的比例,从而能更好地帮助学生。
写在最后,是让学生记忆零散的知识点,再慢慢地形成自己知识体系。还是把知识点整体化放在习题中记忆,更有利于学生知识的提取呢?需要老师根据自己的教学风格调节二者的比例,从而能更好地帮助学生。
题主所说的“题型教学法”,在高中是很常见。有许多参考资料走的就是“母题”的路子——把一个题当做母题,然后把它的变型题做为“子题”,最后再扩展到类似的题上。
这样学生很容易通过对比找出解题的规律,而且也不容易遗忘。
 1、提取模块而非零碎知识点
1、提取模块而非零碎知识点它的处理思路就是,在类比中记住了习题,记住了它们,也就记住知识点和知识点的关联方式。
就如同把许多基础知识放到了一个个的盒子里面,我们记忆的和提取的是不同的盒子。这比单纯记忆零散的知识效率要高得多。
斯科特•扬在《如何高效学习》中提出了整体性学习法。核心观点就是:在知识之间创造联系,会记得越牢、理解得越好,也越容易掌握并应用这些知识。提高学习效能的一个关键途径就是将知识模块化。
象棋大师并非记忆力超群,他们之所以看得步骤比普通人多,就是因为他们的知识是模块化的——几个步骤是存放在一起的。
题主所说的数学题型话教学就是,让学生对某种题型产生整体性记忆。
 2、稳中求变
2、稳中求变此法会不会僵化学生思维,使学生机械化呢?
刚开始确实是这样,可是随着学生学习的深入,这些模块的知识会成为他们思维的中流砥柱。这就是稳。
当再次解决类似的问题,知识点的连接方式会有稍微的不同。而这些差异会与他们原有记忆模块产生冲突,这会让他们的思维边界不断地扩展。
换句话说,在稳定之后,其它的变化是可控的。
还有一点,我们不能只强调老师的作用。我们还要考虑学生的主动性。
当孩子在老师引导下,发现数学在某些规律下运作时,他们也会积极主动的钻研的,极有可能突破老师所教学方法的束缚。
 写在最后,是让学生记忆零散的知识点,再慢慢地形成自己知识体系。还是把知识点整体化放在习题中记忆,更有利于学生知识的提取呢?需要老师根据自己的教学风格调节二者的比例,从而能更好地帮助学生。
写在最后,是让学生记忆零散的知识点,再慢慢地形成自己知识体系。还是把知识点整体化放在习题中记忆,更有利于学生知识的提取呢?需要老师根据自己的教学风格调节二者的比例,从而能更好地帮助学生。
- 发表于 2022-03-24 16:18
- 阅读 ( )
- 分类:教育
今天,有什么经验需要分享呢?
立即撰写